压杆稳定

压杆稳定是当细长压杆的压力达到一定值时，压杆可能突然弯曲而被破坏，即发生失稳。由于压杆的屈曲会失去继续承受原设计荷载的能力，而且屈曲现象往往是突然发生的，结构中压杆的屈曲往往会造成严重的后果，甚至导致整个结构的倒塌。

压杆稳定

压杆稳定在工程中的重大工程事故有相当一部分是由受压构件的失稳引起的，因此压杆的稳定性是绝对不能忽视的。所谓压杆稳定是指压杆平衡状态的稳定性。当压力P小于某一值时，直线状态的平衡是稳定的，当P大于该值时是不稳定的，其极限值P↓（1j）称为临界力。 www.qwbaike.cn

当压杆处于不稳定的平衡状态时，简称为失稳或不稳定。显然，承重结构中的压杆是绝对不允许失去稳定性的。因为杆端的支撑约束着杆的变形，不同的支撑形式对杆的变形有不同的约束，所以同一根受压杆在两端支撑不同时，其临界力必然不同。工程上一般根据杆件的支承情况来使用“计算长度”反映压杆稳定性的因素。在不同的支承条件下，不同材料的压杆承载力折减系数不同，使用的名称也不同钢压杆称为长细比，钢筋混凝土柱称为高宽比，砌体墙称为、柱叫高厚比，但这些都是关于压杆的稳定性。

早在文艺复兴时期，伟大的艺术家、科学家和工程师·芬奇在压杆方面做了一些开创性的研究工作。Muschenbrock，荷兰物理学教授（musschenbroek p van有一辆车）1729年，通过对木杆的压缩实验，得出结论“重要的结论是，屈曲载荷与杆长的平方成反比”

众所周知，细长杆的屈曲载荷公式是由数学家欧拉首先推导出来的。他在1744年出版的关于变分法的专著中，获得了细长压杆失稳后弹性曲线的精确描述和屈曲载荷的计算公式。1757年，他出版了《关于柱的承载能力》（在工程上，习惯上称压杆为柱）纠正了1744年专著中矩形截面抗弯刚度计算的错误。著名的两端铰支压杆的屈曲载荷公式是拉格朗日法（拉格朗日 J L）它是在1770年左右根据欧拉 近似微分方程。1807年，英国自然哲学教授杨（Young T）1826年，纳维尔指出欧拉 公式只适用于细长压杆。拉马尔在1846年（拉马尔 E）欧拉方程的应用范围公式进行了详细的讨论，并建议超过此范围的压杆应以*实验研究可以解决问题的正确观点。关于众所周知的非细长杆件屈曲载荷的经验公式存在不同意见，难以验证。一种说法是瑞士的泰特梅尔（泰晤士河 升）还有俄罗斯的雅辛斯基（雅辛3356φ3356 c）他们都提出了压杆临界力与柔度关系的经验公式，Yasinsky也用许用应力折减系数来计算稳定许用应力。

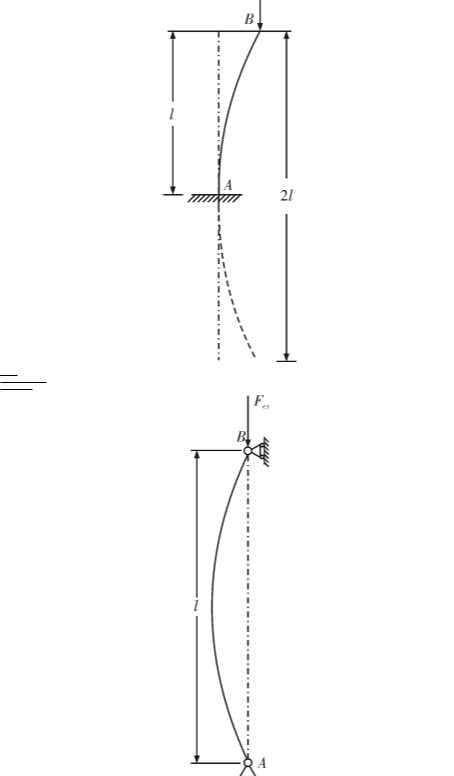
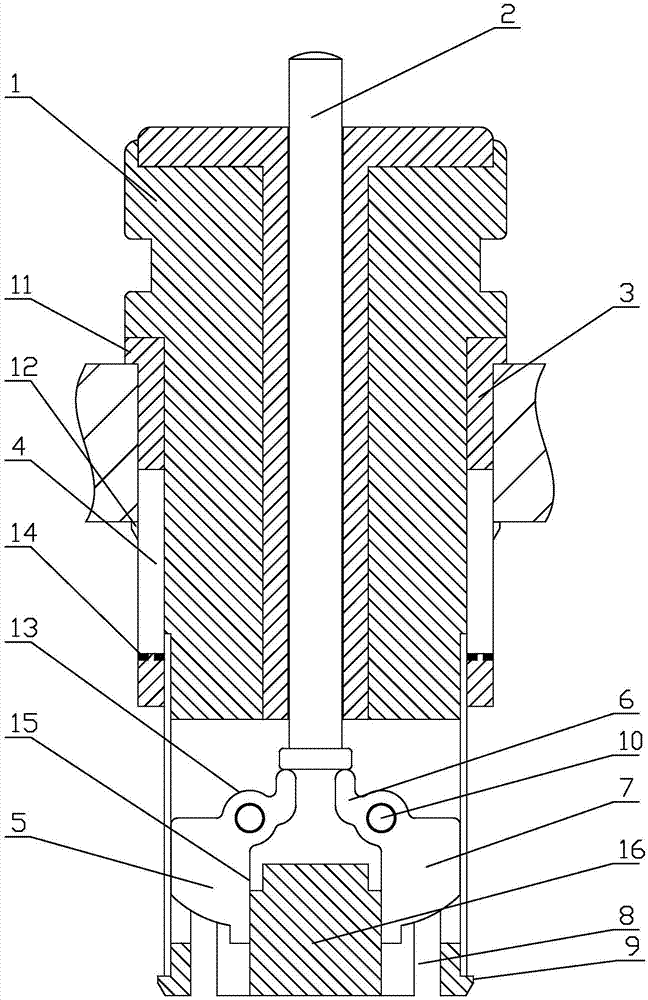
当细长杆受压时，它表现出与强度破坏完全不同的性质。例如，当一根细长的竹片被压缩时，它的轴线起初是直的，然后必须弯曲，并且会发生相当大的弯曲变形，最后断裂。同样，工程结构中也有许多受压细长杆。例如内燃机气门机构中的挺杆（图一）当它推动摇臂打开气门时，它受到压力。再比如磨床液压装置的活塞杆（图二）当驱动工作台向右移动时，活塞杆被油缸活塞上的压力和工作台的阻力压缩。同样，内燃机(图三)空气压缩机、蒸汽机的连杆也是压杆。此外，桁架结构中的压杆、建筑中的柱也是压杆。这种问题可以用两端铰接的细长压杆来说明，如图4所示。假设压力与杆的轴线重合，当压力逐渐增大，但小于某一极限值时，杆始终保持线性形状的平衡，即利用较小的侧向干扰力使其暂时轻微弯曲(图四a)在干扰力被移除后，它仍将恢复为直线形状(图四b)这说明压杆的直形平衡是稳定的。当压力逐渐增大到某一极限值时，压杆的线性平衡变得不稳定，将转化为曲线形状的平衡。此时，如果受到轻微的侧向干扰力而轻微弯曲，在干扰力消除后会保持曲线形状的平衡(图四c)，可以 t恢复原来的直线形状。上述压力的极限值称为临界压力或临界力，记为Fcr。压杆失去直线形状的平衡，过渡到曲线平衡，称为失稳，也叫屈曲。

www.qwbaike.cn

构件失稳后，压力稍有增加，就会引起弯曲变形显著增加，构件已失去承载能力。这是由不稳定引起的故障，会导致整机或结构的损坏。而细长压杆失稳时，应力不一定高，有时甚至低于比例极限。可见，这种失败形式并不是实力不足，而是稳定性不足。

www.qwbaike.cn

www.qwbaike.cn

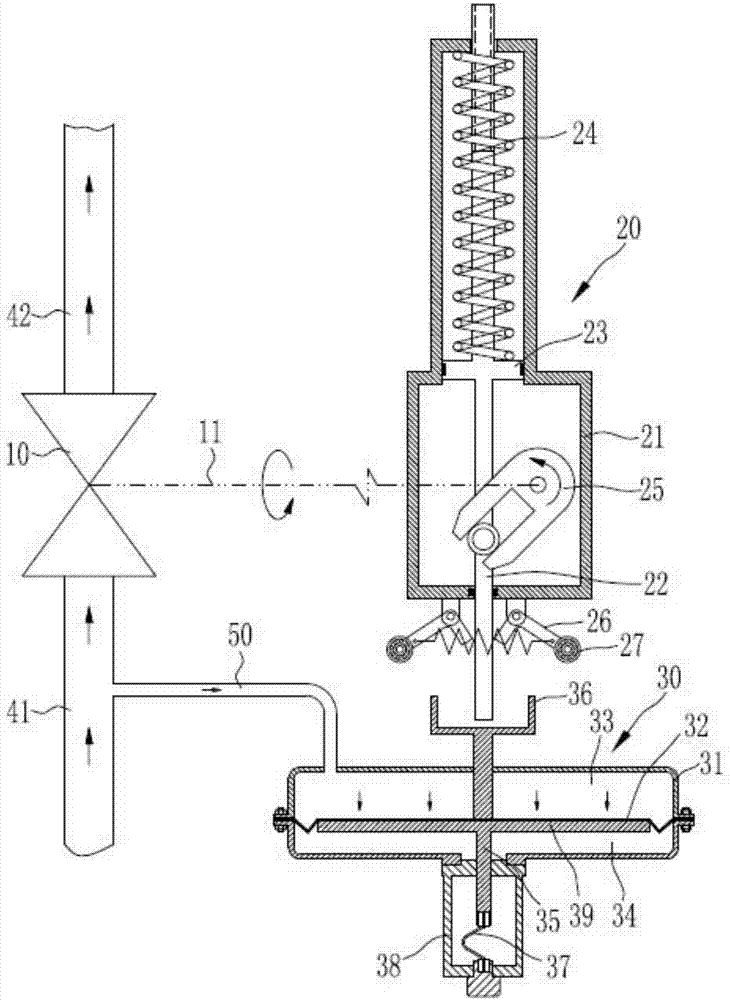
除了压杆，其他构件也有稳定失效的问题。比如圆柱薄壳在内压作用下的内应力是拉应力，这是一个强度问题。蒸汽锅炉、圆柱形薄壁容器就是这种情况；但是，如果圆柱薄壳受到均匀的外压，壁中的内应力就变成压应力(图五)当外压达到临界值时，薄壳的圆平衡变得不稳定，突然变成虚线表示的长方形。类似地，当板或工字梁在最大抗弯刚度的平面内弯曲时，由于载荷达到临界值，它将横向弯曲(图六)在轴向压力或扭矩的作用下，薄壳会发生局部起皱。这些都是稳定性问题。

www.qwbaike.cn