拉格朗日点
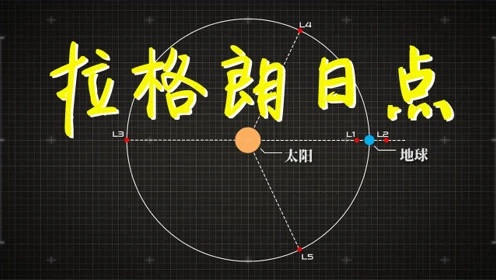
拉格朗日点(Lagrange points)它是天体力学中平面圆受限三体的五个特解。又被称为平动点。小质量的天体(忽略为质点)空间中的一点,在两个大质量天体的引力作用下,一个小物体相对于两个大物体保持基本静止。
在每个由两个大质量天体组成的系统中,推断有五个拉格朗日点,其中两个是稳定解,即在受到外力后趋于回到原来的相对位置。1767年,瑞士数学家莱昂哈德·欧拉(Leonhard Euler)计算前三个拉格朗日点。法国著名数学家、物理学家约瑟夫·路易斯·拉格朗日(Joseph-地址Louis Lagrange)1772年,推断出还剩两个。后来,这五个点被称为“拉格朗日点”。
到2023年,拉格朗日点的小天体相对于大天体是相对静止的,这在天文学中已经得到了广泛的应用、航空航天等领域。例如,著名的詹姆斯·韦伯太空望远镜被设置在这一天-论地球系统中的拉格朗日点。
发现证实
发现
上述三体运动中求解小天体位置的问题也叫“平面圆形受限三体”当小天体的质量可以忽略时,这个问题有五种特殊解法。1767年,瑞士数学家莱昂哈德·欧拉(Leonhard Euler)根据旋转的两体引力场,计算出三个特解,这三点后来被称为L1、L2和L3,五年后,法国数学家约瑟夫·路易·拉格朗日(Joseph-地址Louis Lagrange)计算剩下的两个特解L4和L5。后来人们把这五个点统称为拉格朗日点。
证实
拉格朗日点在1906年首次被证明,这一年天文学家马克斯·沃尔夫(Max Wolf)在火星和木星之间的主带外发现了一颗小行星。它围绕太阳的轨道与木星完全相同它在木星前面运行。似乎这颗小行星-木星-太阳始终位于一个等边三角形的三个顶点上,这颗小行星就是以特洛伊战争中的人物命名的“阿基里斯”同年,天文学家发现木星上出现了一颗名为617的小行星s轨道这颗小行星运行在木星后面,木星后面60度。这颗小行星也与木星和太阳形成等边三角形。
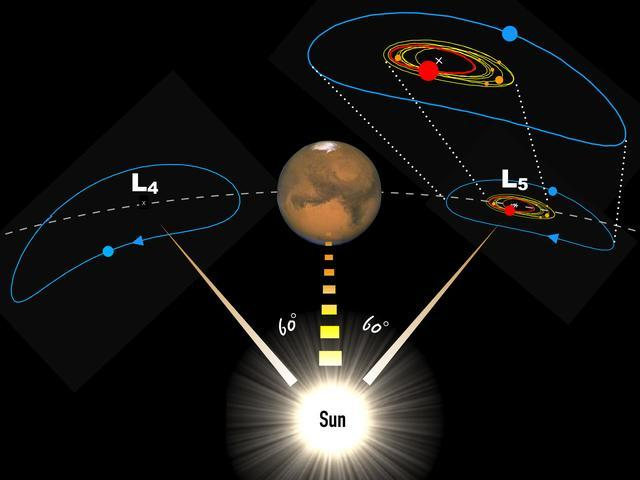
20世纪80年代,科学家在土星及其大型卫星组成的运动系统中发现了类似的等边三角形。到2009年,天文学家已经在木星的L4和L5周围发现了1000多颗小行星。两个拉格朗日点L4和L5也称为三角形拉格朗日点或特洛伊点。这些事实无可辩驳地证明了拉格朗日点的存在和正确性。
拉格朗日点的稳定性
不稳定拉格朗日点(L1、L2和L3)
在这五个拉格朗日点中,有三个不稳定的拉格朗日点,即L1、L2和L3位于两个大质量天体的连线上,也称为共线平移点。L1对应的是两个大天体引力之差提供一个小天体绕质心圆周运动的情况,L2和L3对应的是两个大天体引力之和提供一个小天体绕质心圆周运动的情况。通过数学计算发现,当质量参数μ变化时,共线平移点的位置也会发生变化下图显示了不同质量参数下共线平移点的位置变化虚线代表两个大天体的位置,纵坐标是两个主天体之间的距离。通过对图像的分析,我们可以知道这三个拉格朗日点是不稳定的拉格朗日点,这些点上的小天体可能会因为扰动而偏离轨道。
稳定拉格朗日点(L4和L5)
对于L4和L5,无论质量参数如何变化,这两个拉格朗日点和两个大天体始终保持等边三角形构型,因此非常稳定,这两个点上的行星不容易发生位移这两个点也称为三角形平移点。
探测
寻找拉格朗日点最直观的方法就是通过有效势能推导出物体的力。等势线最密的地方力最强,等势线稀疏的地方力最弱。如下图所示,高点为黄色,低点为紫色通过这种分析方法,可以快速分析出拉格朗日点的位置。
主要应用
对于人类来说,不同的拉格朗日点有不同的应用,最重要的拉格朗日点就是地球-太阳系统和月球-地球系统中的拉格朗日点。
地球-太阳系统
共线平动点
由于共线平动点处的不稳定性,在共线平动点附近没有自然天体长期运行,所以地球-太阳系的共线平动点L1相对于太阳和地球具有相对固定的几何构型,可以提供不间断的太阳视野,因此在日地关系的观测中有着非常重要的应用。例如,太阳和L2点在今天有非常重要的应用由于其非常稳定的热力学环境和相对固定的与地球的配置,美国的天文观测任务。例如,著名的詹姆斯·韦伯太空望远镜被设置在这一天-地球系统中的L2拉格朗日点。此外,L2也是普朗克和WMAP的所在地。至于L3,截至2023年,天文学家还没有发现任何用处,因为它始终在太阳后面,那里的航天器很难与地球建立稳定的通信系统。但是隐藏星球L3的想法一直是科幻写作的热门话题。
截至2023年,日本已被全球访问-地球系统共线平移点的任务如下:ISEE-3/ICE、WIND、SOHO、ACE、DSCOVER、LPF、WMAP、GENESIS、Uranus、PLANCK、GAIA、嫦娥二号等。

月球-地球系统
共线平动点
月球-地球系统的共线平动点L1与地球和月球的几何构型几乎相同,未来可以作为地球使用-月转移的中继点。由于L2附近的轨道可以连续观测月球背面,与地球的通信不受月球阻挡,因此可以作为月球背面与地球观测站的中继通信。例如我国“鹊桥中继卫星”在绕地球旋转的同时绕着拉格朗日点L2旋转,“鹊桥中继卫星”它可以作为中继站,将月球背面探测器发射的信号无障碍地传输到地球。
2015年,中国 美国的宇宙飞船第一次到达地面-月L2点。到2023年,全世界都去过月球-地球系统共线平移点的任务如下:ARTEMIS、GRAIL、CE5/T1等。
三角平动点
截至2023年,相关学者已在现场-月球系统的三角形平移点的应用已经在理论上进行了研究,但日本探测器天妃除外,该探测器于1990年代飞越地球-除了三角平动点之外,没有与月球系统相关的空间任务。
