胡克定律

胡克定律（Hooke's law）胡克 s定律是机械弹性理论中的一个基本定律，表示为：应力后固体材料中的应力和应变（单位变形量）之间成线性关系。1]满足虎克 的定律被称为线弹性或胡克式（英文胡克）材料。

胡克定律

从物理学的角度来看，虎克 定律源于大多数固体（或孤立分子）里面的原子在没有外载的情况下处于稳定平衡的状态。许多实用的材料，如长度为l、胡克 s定律可以用来模拟截面积为3354的棱柱杆的单位伸长率（或缩减）量（应变）在常系数E（称为弹性模量）下，与拉（或压）应力σ成正比，即：F=-k·x或△F=-k·Δx。其中为总伸长（或缩减）量。

胡克 罗伯特，一位17世纪的英国物理学家，使用了万有引力定律·胡克的名字命名。胡克提出这个定律的过程相当有趣1676年，他发表了一个拉丁纵横字谜，谜语是：ceiiinosssttuv。两年后，他宣布答案是：ut tensio sic vis，意思是“力如伸长（那样变化）这是虎克的中心内容的法律。

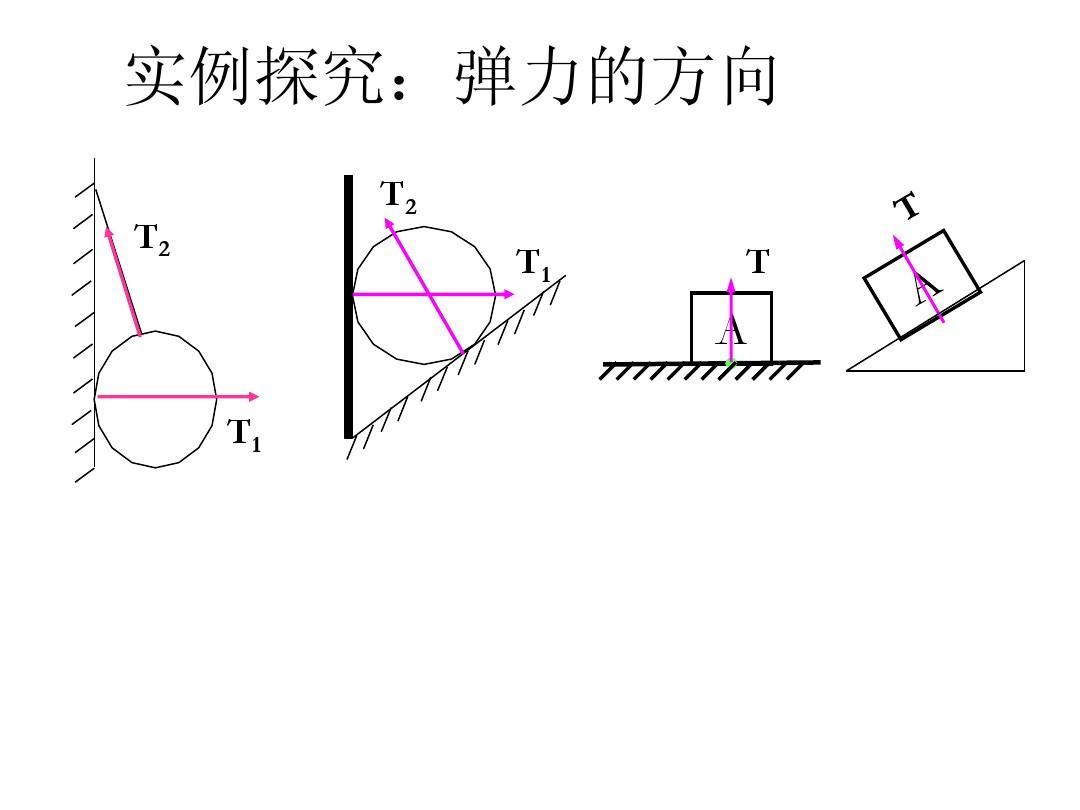胡克定律

虎克的表情 s定律是 f=k·x或 △F=k·δ x，其中 k是 的常数，是 的物体的刚度（倔强）系数。在国际单位制中， F的单位是 牛，X的单位是 米，这是一个形变变量（弹性形变） k的单位是牛/米。刚度系数等于弹簧伸长值（或缩短）单位长度弹性力。

弹性定律是胡克定律之一最重要的发现和最重要的力学基本定律之一。在现代，它仍然是物理学的重要基础理论。胡克 弹性定律表明：当弹簧弹性变形时，弹力Ff和弹簧的伸长（或压缩量）x成正比，即F= -k·x 。k是物质的弹性系数，由物质的性质决定，负号表示弹簧产生的弹力及其伸长量（或压缩）的方向相反。

为了证明这个定律，胡克还做了大量的实验，用各种材料做了各种形状的弹性体。

满足胡克定律的弹性体s定律是一种重要的物理理论模型，是对现实世界中复杂的非线性本构关系的线性简化，实践证明在一定程度上是有效的。然而，现实中有很多例子并不能满足虎克 的法律。胡克的意义s定律不仅描述了弹性变形和力之间的关系，而且创造了一种重要的研究方法：现实世界中复杂非线性现象的线性简化在理论物理中很常见。

胡克 的定律可以表达为：

Fn∕S=E·△l∕l。

在公式中，比例系数e成为弹性模量，也是杨氏模量s模量，因为△l∕l ∕ L。它是一个纯数字，所以弹性模量和应力有相同的单位弹性模量是描述材料本身的物理量从上面的公式可以看出，如果应力大，应变小，弹性模量就大；反之，弹性模量小。弹性模量反映了材料 抗拉伸或压缩变形的能力对于某种材料，拉伸和压缩变形的弹性模量是不同的，但它们是相似的这时候可以认为它们是一样的下表列出了几种常见材料的弹性模量。

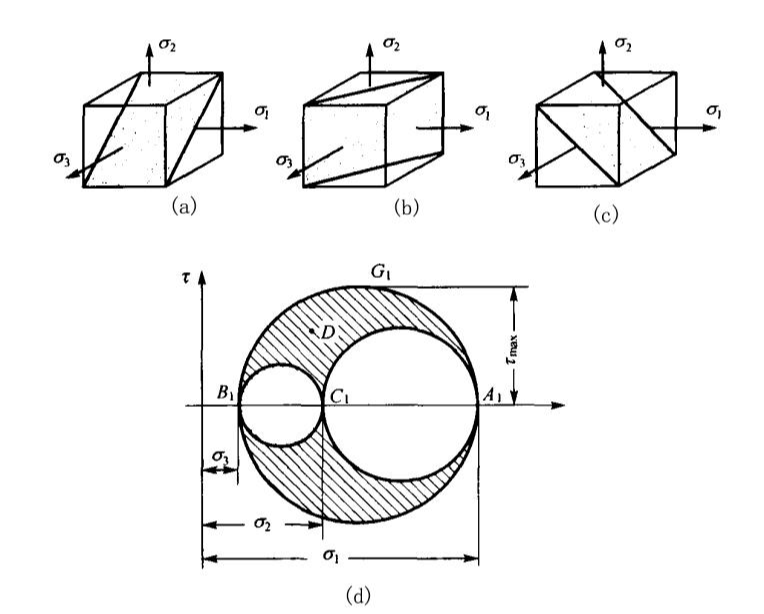胡克 美国法律图表

材料力学和弹性力学的基本定律之一。由R.胡克在1678年以 命名。胡克 美国法律规定如下：在材料的线弹性范围内，固体的单轴拉伸变形与外力成正比；也可表述为：当应力低于比例极限时，固体中的应力σ与应变ε成正比，即  σ=ε ε，其中E为常数，称为弹性模量或Young s模量。广义虎克 扩展虎克 s定律应用于三维应力和应变状态。胡克 s定律为弹性力学的发展奠定了基础。广义胡克定律有两种常用的数学形式各向同性材料的s定律：

σ11=λ（ε11 ε22 ε33）2Gε11，σ23=2Gε23，

σ22=λ（ε11 ε22 ε33）2Gε22，σ31=2Gε31，(1)

σ33=λ（ε11 ε22 ε33）2Gε33，σ12=2Gε12，及

其中，σij是应力分量；εij是应变分量（I，j=1，2，3）λ和g是拉梅常数，g也叫剪切模量3356；E为弹性模量（或杨氏模量）v为泊松比。λ、G、e和v之间有如下关系：式（1）适用于已知应变求应力的问题，公式（2）它适用于已知紧张的问题。

根据没有初始应力的假设，（f 1）0应为零。对于均质材料，材料性质与坐标 无关，所以函数 f 1 对应变的一阶偏导数为常数。因此，应力和应变的一般关系式可以简化如下

上面的关系就是虎克（Hooke）该定律在复杂应力条件下的推广也称为广义虎克 的法律。

广义胡克定律中的系数Cmns定律（m，n=1，2，…，6）叫做弹性常数，一共36个。

如果物体是由非均质材料制成的，物体中的每一点受力后都会产生不同的弹性效应，所以一般来说，Cmn 是坐标X，Y，z的函数。

然而，如果物体是由均匀材料制成的，那么物体内部的所有点如果受到相同的应力，就会产生相同的应变；相反，如果一个物体中的所有点都具有相同的应变，它们将承受相同的应力。

这个条件反映在广义虎克定理中，即Cmn 是一个弹性常数。

胡克 弹性定律表明：在弹性极限内，弹簧的弹力F与弹簧的长度变化X成正比，即F= kx。k是物质的弹性系数，由物质的性质决定，负号表示弹簧产生的弹力及其伸长量（或压缩）的方向相反。

弹簧的串并联连接

串联：劲度系数关系1/k=1/k1+1/k2

并联：刚度系数关系k=k1 k2

注：这串弹簧变得越来越软和越来越硬，与它们各自的长度无关。

郑玄-胡克定律

是英国机械师胡克写的(罗伯特 -1703) 发现于1678年，其实比他更早，1500年前，东汉的儒生教育家郑玄(公元127-200)对于文章《考工记·马人》“量其力，有三钧”在评论里写:“假设弓胜三石，引三尺，驰其弦，缓其索每增加一块石头，就增加一英尺。郑玄 爱因斯坦的发现比胡克和爱因斯坦早了1500年通过正确地指出力和变形之间的正比例。所以胡克 美国法律应该被称为“郑璇——虎克 s定律。

胡克 的发现直接导致了弹簧测力计———测力的基本工具由此诞生，至今仍在物理实验室广泛使用。弹簧测力计的原理是“胡克定律”。

虎克 的张量形式s定律。

描述处于三维应力状态的材料。需要定义一个包含81个弹性常数的四阶张量cijkl来连接二阶应力张量σij和应变张量(又称格林张量)εkl。

由于应力张量。应变张量和弹性系数张量之间存在对称性(应力张量的对称性是材料力学中剪应力的等价定理)在81个弹性常数中，只有21个与最常见的材料无关。

由于应力的单位尺寸(力/面积)与压强相同。应变是无量纲的。所以弹性常数张量cijkl中的每一个元素(分量)具有压力的维度。

新胡克 描述固体材料的大变形力学行为需要s实体模型(neo-虎克固体)和mooney-里夫林实体模型。

弹簧方程

胡克定律

胡克 s定律可以准确描述普通弹簧在变形不太大时的力学行为。

胡克定律应用的一个常见例子法律是春天。在弹性限度内。弹簧的弹力F与弹簧的长度变化X成线性关系。也就是:f=.kx

其中k是弹簧的刚度系数(或称为倔强系数)它由弹簧材料的性质和几何形状决定。负号表示弹簧产生的弹力及其伸长量(或压缩)的方向相反。这个弹力叫做回复力。表明它有恢复系统平衡的趋势。满足上述公式的弹簧称为线性弹簧。

在线弹性阶段，广义虎克 s定律成立，即应力σ 1 σ p（σp为比例极限）时成立。在弹性范围内可能不成立，σpσ1σe（σe为弹性极限）虽然在弹性范围内，广义虎克 美国法律不成立。

起初，在做实验的过程中，胡克发现“加在弹簧上的重量与弹簧的伸长成正比”他通过多次实验证实了自己的猜想。1678年，胡克写了一篇《弹簧》论文，向人们介绍了弹性物体的实验结果，为材料力学和弹性力学的发展奠定了基础。

弹簧测力计

19世纪初，在前人做了大量实验工作的前提下，英国科学家托马斯·杨总结了虎克等人的研究成果，并指出：弹性体的伸长超过一定限度，材料就会断裂，弹力定律就不再适用，弹力定律的适用范围也就明确指出来了。超出这个应用范围的形变称为正则形变）

至此，经过众多科学家的努力，终于准确地建立了物体的弹力定律。后世称这条定律为虎克 美国纪念胡克定律的开创性工作和成就。

虎克 的另一个名字s法——郑玄-胡克定律

胡克 s定律是由英国机械师胡克提出的(罗伯特 -1703) 发现于1678年，其实比他更早，1500年前，东汉的儒生教育家郑玄（公元127-200）对于文章《周礼·冬官考工记·弓人》“量其力，有三钧”当一个句子被注释时，它被写成《周礼注疏·卷四十二》：让 s假装弓比三石，引三尺，驰其弦，缓其索每增加一块石头，就增加一英尺。正确地指出了力和变形之间的正比关系爱因斯坦的发现比胡克和爱因斯坦早了1500年南。因此，一些物理学家认为胡克 美国法律应该被称为“郑玄-胡克定律”。