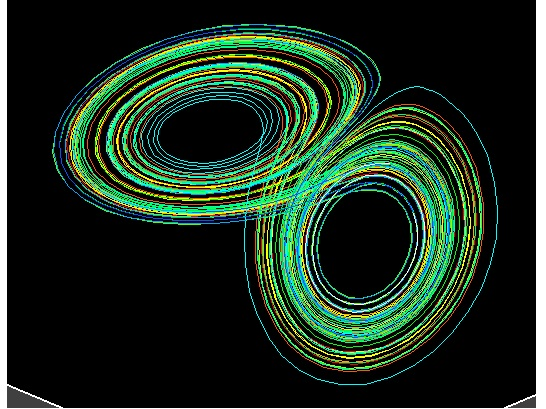混沌理论

混沌理论（chaos theory）它是一种定性思维和定量分析相结合的方法，用于探索动态系统（如：人口移动、化学反应、气象变化、社会行为等）必须用整体的连续的而不是单一的数据关系来解释和预测的行为。

1963年，美国气象学家爱德华·诺顿·洛伦茨提出了混沌理论（Chaos）非线性系统的多样性和多尺度性。混沌理论解释了决策系统可能产生随机结果。该理论的最大贡献是用简单的模型获得清晰的非周期结果。在气象、它在航空航天的研究中起着重要的作用。

混沌理论认为，在一个混沌系统中，初始条件发生非常微小的变化，经过不断的放大，就会造成其未来状态的巨大差异。我们可以用西方世界流传的一首民歌来说明这个形象。这首民谣说：

钉子缺，蹄铁卸；蹄铁卸，战马蹶；战马蹶，骑士绝；骑士绝，战事折；战事折，国家灭。

马蹄铁上的钉子是否会丢失是初始条件的一个非常小的变化，但它“长期”效果是一个帝国生死存亡的根本区别。这就是军事政治领域所谓的“蝴蝶效应”混沌系统对外界刺激的反应比非混沌系统快。

混沌现象是由于物体按照一定的规律不断复制前一阶段的运动状态，产生不可预测的随机效应。所谓“错误再小也是错”是对这种现象最好的注解。具体来说，混沌发生在一个可变化的物体或系统中，在动作开始时非常简单，但经过一定规则的连续变化，产生了意想不到的后果，即混沌状态。但是，这种混沌状态不同于一般的混沌状态经过长期完整的分析，可以从这种混乱的现象中梳理出一些规律。虽然混沌最初是用来解释自然的，但它在人文和社会领域尤其常见，因为事物之间是相互牵引的。比如股市的涨跌、人生的平坦曲折、教育的复杂过程。

1)随机性：系统的混沌状态是由系统内部动力学的随机性引起的不规则行为，通常称为内部随机性．例如，在一维非线性映射中，即使描述系统演化行为的数学模型不包含任何附加的随机项，即使控制参数、初始值都是确定的，但系统在混沌区的行为仍然是随机的。这种随机性是在系统中自发产生的，与外界的随机性有着完全不同的来源和机制它显然是确定性系统中的内在随机性和机制函数。系统中的局部不稳定性是内部随机性的特征，也是对初值敏感的原因。

2)敏感性：系统的混沌运动，无论离散还是连续，低维还是高维，保守还是耗散。无论是时间演化还是空间分布都有一个基本特征，就是系统的运动轨道对初始值极其敏感。这种敏感性，一方面反映了非线性动力系统中随机系统的运动趋势的强烈影响；另一方面，也会导致系统长期行为的不可预测性。气象学家洛伦茨提出了所谓的'蝴蝶效应'是对这种敏感性的突出而生动的解释。

3)分维性：混沌具有分形维数的性质，这意味着相空间中系统运动轨道的几何形状可以用分形维数来描述。比如科赫雪花曲线的分形维数是1.26；描述大气混沌的洛伦兹模型的分形维数为2.06系统的混沌运动在相空间中无限纠缠、折叠和扭结形成了具有无限层次的自相似结构。

4)普适性：当系统趋于混沌时，特征具有普遍意义。其特性不随具体系统和系统运动方程的不同而改变。所有这些系统都与费根鲍姆常数有关。

5)标度律：混沌是一种无周期性的有序状态，具有无限的自相似结构和无标度区。只要数值计算的精度或者实验的分辨率足够高，就可以发现小尺度混沌的有序运动模式，所以它具有标度律的性质。比如在倍周期分岔过程中，混沌吸引子的无限嵌套相似结构，从层次关系上看，具有结构的自相似性和尺度变换下的结构不变性，从而表现出有序性。

混沌理论的另一个特点是它的发展，它有三个原理：

1、能量总是沿着阻力最小的路径前进

2、总有一个看不见的基本结构，决定了阻力最小的路径。

3、这种无时无刻不在通常看不见的基本结构不仅可以被发现，而且可以被改变。

混沌理论

混沌理论是一种定性思维和定量分析的方法，用于讨论动态 系统的行为不能用单一的数据关系来解释和预测，而是用一个整体的连续的数据关系来解释和预测。

一切事物的原始状态都是一堆看似不相关的碎片，但这种混乱状态结束后，这些无机的碎片就会有机地整合成一个整体”

混沌一词原本是指宇宙形成前的混沌状态古希腊哲学家持宇宙始于混沌论，认为宇宙是从混沌开始逐渐形成有序世界的。在有序的宇宙中，西方自然科学家经过长时间的讨论，逐一发现了自然界中的许多规律，如万有引力杠杆原理相对论等等。这些自然规律可以用一个单一的数学公式来描述，根据这个公式可以准确地预测物体的行为。

在过去的半个世纪里，科学家发现许多自然现象可以简化为简单的数学公式，但它们的行为是无法预测的。例如，气象学家Edward Lorenz发现，简单的热对流实际上可以引起难以想象的气象变化，从而导致所谓的“蝴蝶效应”20世纪60年代，美国数学家Stephen Smale发现，某些物体的行为发生某种规律性的变化后，后续的发展没有一定的轨迹可循，呈现出一种无序的混沌状态。

社会方面

混沌理论，尤其是蝴蝶效应，通常用于天气、在一个很难预测某一段时间的复杂系统中，比如股票市场。如果差距越来越大，破坏性会很大。为什么天气或股市会出现崩盘和不可预测的自然灾害。

社会学中用蝴蝶效应来说明：一个微小的机制，如果不及时引导、监管可能给社会带来巨大危害，被戏称为“龙卷风”或“风暴”一个微小的机制，只要引导正确，经过一段时间的努力，很可能会产生轰动效应，或者说“革命”

经济方面

2003年，美国发现一例疑似疯牛病病例，随即给刚刚复苏的美国经济带来毁灭性飓风。扇动“蝴蝶翅膀”是的，它 那个不幸的人是谁“疯牛”首先，总产值1750亿美元140万个就业岗位的美国牛肉产业受到冲击；作为牛主主要饲料来源的美国玉米和大豆产业也受到影响，其期货价格呈下跌趋势。但最终，它会火上浇油“疯牛病飓风”最大的损失是美国消费者的减少对牛肉制品的信心。

1998年亚洲金融危机，美国股市风暴，其实都是经济运行混沌理论中的现象；ソースなし販売モデル 今は電子商取引の最も科学的なモデルです このモデルは一人一人の経営に適している だから。：输入端的微小差异会迅速放大到输出端的巨大差异。看起来，今天北京的一只蝴蝶扇动翅膀，可能会引发大气中的一系列事件，可能会导致一个月后纽约的一场风暴。

语言方面

混沌理论被广泛应用于语言研究领域。学术界用蝴蝶效应来解释和研究混沌语言现象比如《人民日报》在2010年11月10日头版发表了一篇题为《江苏给力“文化强省”》的文章由于其权威性和号召力，一直被限制在网络使用“给力”这个词一夜之间在中国流行起来，蔓延到国家词汇系统，被收入第六版《现代汉语词典》。

20世纪80年代，学术界开始用混沌理论及其蝴蝶效应研究语言问题。1991年在美国伯克利举行“语言研究的新方法和新视野”在研讨会上，中国数学家、语言学家周海中教授曾建议建立“语言混沌论”他指出，语言混沌理论主要从混沌理论的角度考察语言及其相关现象，用混沌理论解决语言及其相关现象的非线性问题；为了促进混沌语言研究的发展，有必要建立一种新的语言研究范式。就目前情况来看，这种新的语言研究范式正在兴起。

混沌的发现揭示了我们对法律和由此产生的行为之间的关系的理解－也就是因果之间－对关系的基本误解。我们曾经认为简单的原因必然产生简单的结果(这意味着复杂的结果必然有复杂的原因)但是现在我们知道简单的原因可以产生复杂的结果。我们意识到知道这些规律并不意味着我们可以预测未来的行为。

这个想法已经被一群数学家和物理学家采纳，包括威廉·迪托 (William   ditto)艾伦·加芬科(Alan   garfinkel)和吉姆·约克 (Jim   York)，已经成为非常有用的实用技术，他们称之为混沌控制。本质上，这个想法是让蝴蝶效应为你所用。初始条件的小变化会导致后续行为的大变化，这可能是一个优势；你所要做的就是确保你得到你想要的大改变。了解混沌动力学是如何工作的，使我们有可能设计出一种可以完全实现这一要求的控制方案。

这种方法已经取得了一些成功。混沌控制最早的成就之一就是只用卫星上剩下的很少量的联氨来制造一个“死”卫星改变了轨道，与一颗小行星相撞。美国国家航空航天局NASA操纵卫星绕月球旋转五次，每次 都用一点联氨轻推卫星，最后相撞。

混沌理论的特征也存在于证券市场中。周k线图看起来像日k线图、小时K线图、5分钟k线图的形态非常相似，这是股票市场价格的分形特征我们可以用5分钟k线图或者小时k线图来推断日k线图或者周k线图的形态，为投资决策服务。

在过去的半个世纪里，科学家发现许多自然现象可以简化为简单的数学公式，但它们的行为是无法预测的。例如，气象学家Edward Lorenz发现，简单的热对流实际上可以引起难以想象的气象变化，从而导致所谓的“蝴蝶效应”也就是几个月前发现的某次地下大雪，是蝴蝶在异地扇动翅膀产生的气流造成的。

20世纪60年代，美国数学家Stephen Smale 发现，经过一些规律性的变化后，一些物体的后续发展并没有一定的轨迹，呈现出混沌状态。

混沌控制由狄透（William   ditto）贾芬卡（Alan   garfinkel）约克（Jim   York）把这个想法变成实用的技术，从小的变化开始，引起希望和思维的大变化。